Discussion 6

Review of last week

# Python3
import sqlite3
conn = sqlite3.connect(NAME)
cursor_obj = conn.cursor()
cursor_obj.execute(SQL_COMMAND)
cursor_obj.fetchall()

Commonly used commands:

SELECT - extracts data from a database
INSERT INTO - inserts new data into a database
DELETE - deletes data from a database
CREATE TABLE - creates a new table
AGGREGATE FUNCTIONS - e.g. AVG, COUNT, MAX, MIN, SUM…
GROUP BY - groups rows that have the same values
JOIN - combine rows from two or more tables
WITH - give a sub-query block a name
UNION - combine the result-set of two or more SELECT statements
HAVING - apply conditions over aggregation functions

SELECT column1, column2, ...
FROM table_name;

SELECT DISTINCT column1, column2, ...
FROM table_name;

SELECT column1, column2, ...
FROM table_name
WHERE condition;

SELECT column1, column2, ...
FROM table_name
ORDER BY column1, column2, ... ASC|DESC;

INSERT INTO table_name
VALUES (value1, value2, value3, ...);

DELETE FROM table_name WHERE condition;

CREATE TABLE table_name (
    column1 datatype,
    column2 datatype,
    column3 datatype,
   ....
);

SELECT MIN|MAX|COUNT|AVG|SUM(column_name)
FROM table_name
WHERE condition;

SELECT count(ID), occupation FROM people_main
GROUP BY occupation;

SELECT column_name(s)
FROM table1
(INNER) JOIN table2
ON table1.column_name = table2.column_name;

Different types of JOIN

people.db.

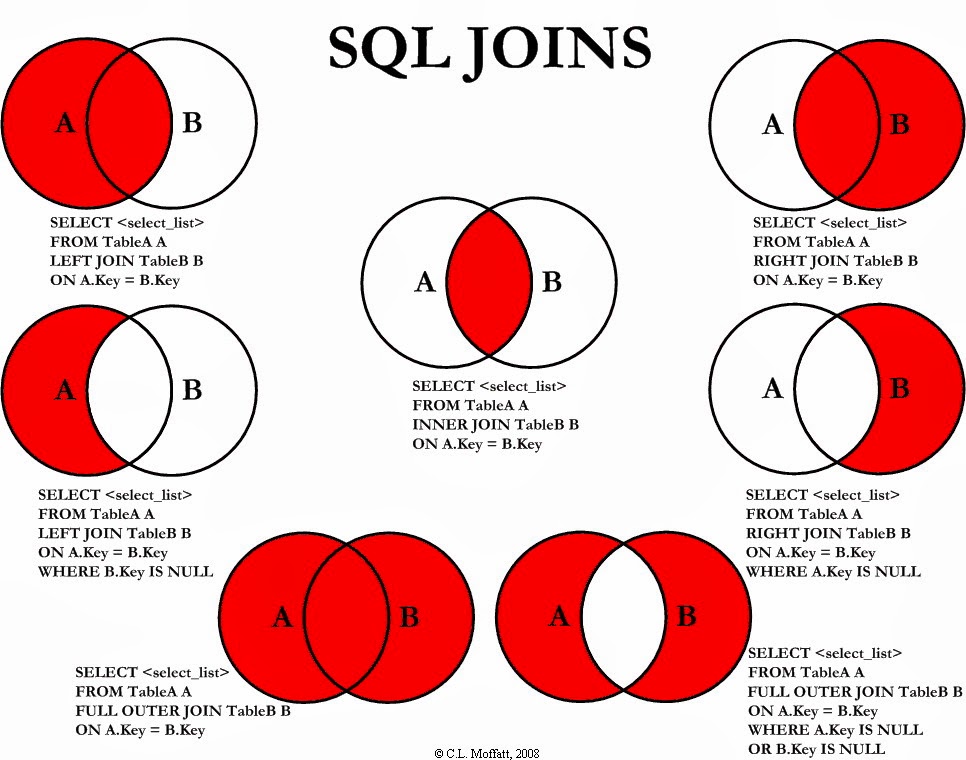
It contains the name, age, ID, and occupation of some students, as well as their relationships. Here are the tables in that database.

people_main(ID INTEGER, name TEXT, occupation TEXT, age INTEGER)
people_likes(ID1 INTEGER, ID2 INTEGER)
people_friends(ID1 INTEGER, ID2 INTEGER)

 (1, 'Pheonix Chambers', 'Chefs', 35),
 (2, 'Shaquille Mcintosh', 'Librarians', 29),
 (3, 'Lailanie Mcfarland', 'Principals', 26),
 ...

 (1, 29),
 (4, 74),
 (4, 100),
 ...

Write a SQL statement to find pairs (A, B) such that person A likes person B, but A is not friends with B. Results should be ordered by ID1 (ascending), then ID2 (ascending).

Hint: consider left join.

WITH

Often times, we want to combine two tables, but one of the tables is the result of another query.

WITH previous_results AS (
   SELECT ...
   ...
   ...
   ...
)
SELECT *
FROM previous_results
JOIN people_main
  ON previous_results.__ = people_main.__;

Exercises

Write a SQL statement that returns the occupation and and how many people like that occupation. Results should be ordered by popularity from high to low

Hint: First join people_main with people_likes, then run group by command with count

Write a SQL statement that returns the distinct name and age of all people who are liked by anyone younger than them. Results should be ordered by name (A-Z)

UNION

The UNION operator is used to combine the result-set of two or more SELECT statements.

SELECT column_name(s) FROM table1
UNION
SELECT column_name(s) FROM table2;

HAVING

The HAVING clause was added to SQL because the WHERE keyword could not be used with aggregate functions.

Example, if I want to know the occupations that have more than 5 people, we can write the query as

SELECT occupation, count(*) FROM people_main
GROUP BY occupation
having count(*) > 5;

Exercise:

Write a SQL statement that returns the name and occupation of all people who have more than 3 friends.

Consider using JOIN, GROUP BY, COUNT and HAVING

Relational database

Different Key types

Primary key is a set of one or more fields/columns of a table that uniquely identify a record in database table. It can not accept null, duplicate values. Only one Candidate Key can be Primary Key.

Foreign key is a field in database table that is Primary key in another table. It can accept multiple null, duplicate values. For more help refer the article Difference between primary key and foreign key.

Practice

Consider the following relational schema:

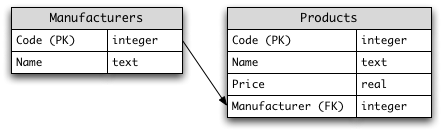
PK and FK stand for primary key and foreign key respectively.

We first generate the tables using the following code:

# In Python
conn = sqlite3.connect('computer.db')
cursor_obj = conn.cursor()
cursor_obj.execute('''
CREATE TABLE Manufacturers (
	Code INTEGER PRIMARY KEY NOT NULL,
	Name CHAR(50) NOT NULL 
);
''')
cursor_obj.execute('''
CREATE TABLE Products (
	Code INTEGER PRIMARY KEY NOT NULL,
	Name CHAR(50) NOT NULL ,
	Price REAL NOT NULL ,
	Manufacturer INTEGER NOT NULL 
		CONSTRAINT fk_Manufacturers_Code REFERENCES Manufacturers(Code)
);
''')
cursor_obj.execute('''
INSERT INTO Manufacturers(Code,Name) VALUES (1,'Sony'),
                                    (2,'Creative Labs'),
                                    (3,'Hewlett-Packard'),
                                    (4,'Iomega'),
                                    (5,'Fujitsu'),
                                    (6,'Winchester');   
''')
cursor_obj.execute('''
INSERT INTO Products(Code,Name,Price,Manufacturer) VALUES
(1,'Hard drive',240,5),
(2,'Memory',120,6),
(3,'ZIP drive',150,4),
(4,'Floppy disk',5,6),
(5,'Monitor',240,1),
(6,'DVD drive',180,2),
(7,'CD drive',90,2),
(8,'Printer',270,3),
(9,'Toner cartridge',66,3),
(10,'DVD burner',180,2);
''')

Now, based on the tables created, finish the following tasks:

Select the names and the prices of all the products in the store.
Select the name of the products with a price less than or equal to $200.
Select the name and price in cents (i.e., the price must be multiplied by 100).
Compute the average price of all the products.
Select the name and price of all products with a price larger than or equal to $180, and sort first by price (in descending order), and then by name (in ascending order).
Select the name and price of the cheapest product.
Select the average price of each manufacturer’s products, showing the manufacturer’s name.

Solutions

Interview questions:

Suppose we throw a fair coin. Which of the following probability is larger: (1) Throw 10 times and get 5 heads. (2) Throw 100 times and get 50 heads.
Suppose we do a simple linear regression without inercept: y ~ x. (1) Will the point estimate of $\hat\beta$ change if we duplicate the data points? (2) Will the $t$-statistic change? If it changes, what is the relationship with before?
Suppose we do a simple linear regression with intercept, and the sample variance of $x_i$ and $y_i$ equals to each other. Consider the following two model: $y = \hat a_1 + \hat b_1 x$; $x = \hat a_2 + \hat b_2 y$. (1) What are the relationships between $\hat b_1$ and $\hat b_2$? (2) What are the relationships between $R^2$ when we run y ~ x and x ~ y? (3) What are the relationship between $\hat b_1$, $\hat b_2$ and $R^2$?
Find an example such that $\text{Cor}(x_1, y) < 0.1$, $\text{Cor}(x_2, y) = 0$, but the $R^2$ for y ~ x1 + x2 equals to 1.